Последовательное соединение конденсаторов
Имея несколько конденсаторов с разными параметрами, можно существенно расширить количество возможных величин емкости и увеличить диапазон рабочего напряжения, соединяя конденсаторов в батареи.
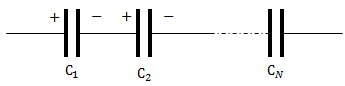
Рис. 1
Последовательное соединение конденсаторов
При последовательном соединении конденсаторов обкладка «номер два» соединятся с первой обкладкой следующего конденсатора (рис.1). Получается, что соседние обкладки конденсаторов образуют единый проводник. На этом проводнике, при включении напряжения на батарее, появляются индуцированные заряды, равные по величине заряду на первой обкладке первого конденсатора и на второй обкладке 2-го конденсатора. Подобная ситуация справедлива для второй обкладки второго конденсатора и первой обкладке третьего и так далее. Получается, что для всех конденсаторов, которые включены последовательно, на обкладках находятся одинаковые заряды. При этом напряжение на каждом из конденсаторов равно:
![]()
![]() – напряжение на конденсаторе номер i, емкость которого
– напряжение на конденсаторе номер i, емкость которого ![]() . Суммарное напряжение равно разности потенциалов, которая приложена к соединению:
. Суммарное напряжение равно разности потенциалов, которая приложена к соединению:
![Rendered by QuickLaTeX.com \[{\varphi}_1-{\varphi}_2=\sum^N_{i=1}{U_i=}\sum^N_{i=1}{\frac{q}{C_i}=}q\sum^N_{i=1}{\frac{1}{C_i}} \qquad (2) \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-104e0335fdfdcac4102c36e8efe99685_l3.png)
Из формулы (2) получается, что электрическая емкость последовательного соединения конденсаторов может быть вычислена по формуле:
![Rendered by QuickLaTeX.com \[\frac{1}{C}=\sum^N_{i=1}{\frac{1}{C_i}} \qquad (3) \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-04dbf1a84a793c75a711c2fbf45cc0a5_l3.png)
Выражение (3) показывает, что при последовательном соединении конденсаторов складывают величины обратные емкостям отдельных конденсаторов. В соответствии с формулой (2) часть суммарного напряжения, которая приходится на рассматриваемый конденсатор, является величиной, обратной его емкости. Следовательно, необходимо, чтобы ни на какой из конденсаторов ни падало напряжение, которое превышает его максимально возможное.
При равенстве емкостей (![]() ) всех конденсаторов в последовательном соединении, и одинаковом предельном напряжении для них всех (
) всех конденсаторов в последовательном соединении, и одинаковом предельном напряжении для них всех (![]() ) емкость батареи составляет:
) емкость батареи составляет:
![]()
Предельное напряжение батареи:
![]()
Примеры решения задач
| Задание | Какими будут заряды на каждом из конденсаторов при их соединении, указанном на рис.2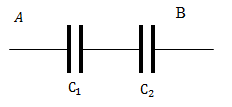
Рис. 2 |
| Решение | Если разность потенциалов на первом конденсаторе равна При последовательном соединении конденсаторов, на каждом из них заряды одинаковы: По определению емкости: Емкость первого конденсатора равна: Емкость второго конденсатора: Выразим заряд q из (1.4) и (1.5), в соответствии с (1.2),имеем: Подставим Из формулы (1.7) получим Найдем искомые заряды: Вычислим искомые заряды: |
| Ответ |
| Задание | Два конденсатора соединены последовательно. Емкость батареи составляет С= |
| Решение | При последовательном соединении:
При последовательном соединении конденсаторов емкость батареи (C) равна: Выразим емкость второго конденсатора: Разность потенциалов на первом конденсаторе равна ( Разность потенциалов на втором конденсаторе ( Проведем вычисления: |
| Ответ |











