Неполярные конденсаторы

Определение и общие понятия о неполярных конденсаторах

ОПРЕДЕЛЕНИЕ

Конденсатором называют систему из двух проводников (обкладок), размещенных близко друг от друга, разделенных диэлектриком.

Толщина диэлектрика, как правило, много меньше в сравнении с размерами обкладок. Конденсатор служит для того, чтобы накапливать заряд (и соответственно энергию электрического поля) и отдавать его. Основными характеристиками конденсатора являются: электрическая емкость (C) и пробивное напряжение (U).

Основу устройства конденсаторов составляет то, что электрическая емкость проводника увеличивается, если к нему приближают другое тело. Это объясняется тем, что под воздействием электрического поля заряженного проводника, на приближенном к нему теле, возникают заряды. Если вторым телом является проводник, то это индуцированные заряды, если тело состоит из диэлектрика, то это связанные заряды. Заряды, равные по величине и противоположные по знаку расположены, при этом, ближе к первому проводнику, чем одноименные. Значит, они оказывают большее воздействие на потенциал первого проводника. Так, при приближении к проводнику, несущему заряд, второго тела, величина потенциала проводника уменьшается. В соответствии с выражением:

$C=\frac{q}{\varphi} \qquad (1)$

это значит, что емкость увеличивается.

Для минимизации влияния внешних тел на емкость конденсатора, его обкладки изготавливают такой формы и располагают так по отношению друг к другу, чтобы поле, которое создают заряды, было локализовано внутри конденсатора. Такому условию удовлетворяют, например, две плоские пластины, разделенные тонким слоем диэлектрика, два соосных цилиндра, две концентрические сферы. По форме обкладок конденсаторы разделяют соответственно: плоские; цилиндрические; сферические.

Так как поле конденсатора заключено, в основном, между его обкладками, то линии электрического смещения начинаются на одной из его обкладок и заканчиваются на другой. При этом сторонние заряды, которые появляются на обкладках, равны по величине и противоположны по знаку.

Конденсаторы являются распространенным элементом электронных схем. Этот элемент может проводить переменный ток и не проводит постоянного тока.

Конденсаторы могут иметь постоянную и переменную емкость, в зависимости от их конструкции. Конденсаторы постоянной емкости делят на полярные и неполярные.

Полярные конденсаторы, к ним относят электролитические конденсаторы, имеют положительный и отрицательный электроды. Для них важно как они включены в цепь. Не соблюдение полярности при включении в состав схемы полярного конденсатора ведет к его выходу из строя. Конденсатор электролитического типа соединяет в себе функции пассивного и полупроводникового элемента.

Неполярные конденсаторы, (или иногда их называют обычными) являются пассивными устройствами, которые служат для накопления заряда, для них не существует ни какой разницы, каким концом элемент включается в электрическую цепь.

Формулы для вычисления емкости конденсатора

Емкость любого конденсатора можно вычислить, используя выражение:

$C=\frac{q}{{\varphi}_1-{\varphi}_2}=\frac{q}{U} \qquad (2)$

где ${\varphi}_1-{\varphi}_2$ – разность потенциалов обкладок конденсатора.

Емкость плоского конденсатора находят как:

$C=\frac{\varepsilon {\varepsilon}_0S}{d} \qquad (3)$

где $\sigma =\frac{q}{S}$ — плотность распределения заряда по поверхности пластины; $\varepsilon$ – диэлектрическая проницаемость вещества, которое находится между пластинами конденсатора; S – площадь каждой (или меньшей) пластины; d – расстояние между пластинами. Формула (3) хорошо соответствует реальности, если расстояние между пластинами много меньше, чем их размеры.

Емкость цилиндрического конденсатора:

$C=\frac{2\pi \varepsilon {\varepsilon}_0l}{ln\left(\frac{R_2}{R_1}\right)} \qquad (4)$

где l – высота цилиндров; $R_2$ – радиус внешнего цилиндра; $R_1$ – радиус внутреннего цилиндра. По формуле (5) вычисляют емкость коаксиального кабеля.

Емкость сферического конденсатора вычисляют при помощи выражения:

$C=\frac{4\pi \varepsilon {\varepsilon}_0R_1R_2}{R_2-R_1} \qquad (5)$

где $R_1{;\ R}_2$ – радиусы обкладок конденсатора.

Емкость в Международной системе единиц (СИ) измеряется в фарадах (Ф).

Примеры решения задач

ПРИМЕР 1

Задание

Какой будет электрическая емкость плоского конденсатора, если пространство между его пластинами заполняют два слоя диэлектрика ( ${\varepsilon}_1,\ {\varepsilon}_2$ ). Толщина первого равна $d_1$ , толщина второго — $d_2$ ? Площадь пластин конденсатора равна S.

Решение

Емкость конденсатора определим как:

$C=\frac{q}{U} \qquad (1.1)$

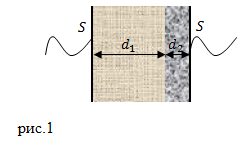
Если посмотреть на рис.1, то можно увидеть, что двуслойный конденсатор, который изображен, можно уподобить двум плоским конденсаторам, которые соединены параллельно. Эти конденсаторы несут одинаковые заряды, площади их обкладок равны (S). Разность потенциалов на «конденсаторе» $C_1$ со слоем диэлектрика ${{\varepsilon}_1,d}_1$ равна $U_1$ , на конденсаторе $C_2$ со слоем диэлектрика ${{\varepsilon}_2,d}_2$ — $U_2$ . При этом разность потенциалов на всем конденсаторе (U) найдем как:

$U=U_1+U_2 \qquad (1.2)$

Используя выражение (1.2) формулу (1.1) запишем как:

$C=\frac{q}{U_1+U_2} \qquad (1.3)$

Заряд q представим как:

$q=\sigma S \qquad (1.4)$

$\sigma$ – поверхностная плотность зарядов на обкладках конденсатора. Величину $U_1$ свяжем с напряженностью электрического поля ( $E_1$ ) в первом слое конденсатора как:

$U_1=E_1d_1=\frac{D}{{\varepsilon}_0{\varepsilon}_1}d_1 \qquad (1.5)$

Для второго слоя конденсатора имеем:

$U_2=E_2d_2=\frac{D}{{\varepsilon}_0{\varepsilon}_2}d_2 \qquad (1.6)$

где D – величина вектора электрического смещения, который не изменяется при переходе через границу диэлектриков. Подставим формулы (1.4) – (1.6) в выражение (1.3), учитывая, что $D=\sigma$ получим:

$C=\frac{\sigma S}{\frac{D}{{\varepsilon}_0{\varepsilon}_1}d_1+\frac{D}{{\varepsilon}_0{\varepsilon}_2}d_2}=\frac{{\varepsilon}_0S}{\frac{d_1}{{\varepsilon}_1}+\frac{d_2}{{\varepsilon}_2}}$

Ответ

$C=\frac{{\varepsilon}_0S}{\frac{d_1}{{\varepsilon}_1}+\frac{d_2}{{\varepsilon}_2}}$

ПРИМЕР 2

Задание

Какова поверхностная плотность зарядов на пластинах плоского конденсатора, если пространство между пластинами конденсатора заполнено веществом с диэлектрической проницаемостью $\varepsilon$ ? Когда конденсатор соединили с источником напряжения, давление пластин на диэлектрик стало равно p.

Решение

По определению давление, которое оказывают пластины на диэлектрик равно:

$p=\frac{\left|F\right|} {S} \qquad (2.1)$

где S – площадь пластин; $\left|F\right|$ – величина силы притяжения, которая действует между пластинами конденсатора. Механическую (пондемоторную) силу, взаимодействия пластин плоского конденсатора находят как:

$F=-\frac{q^2}{2\varepsilon {\varepsilon}_0S} \qquad (2.2)$

В выражении (2.2) минус показывает, что пластины конденсатора притягиваются друг к другу. Подставим (2.2) в формулу (2.1), учтем, что:

$q=\sigma S \qquad (2.3)$

найдем искомую величину:

$p=\frac{\frac{{(\sigma S)}^2}{2\varepsilon {\varepsilon}_0S}} {S}=\frac{{\sigma}^2}{2\varepsilon {\varepsilon}_0}\to \sigma =\sqrt{2\varepsilon {\varepsilon}_0p}$

Ответ

$\sigma =\sqrt{2\varepsilon {\varepsilon}_0p}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Неполярные конденсаторы

Определение и общие понятия о неполярных конденсаторах

Формулы для вычисления емкости конденсатора

Примеры решения задач