Конденсатор в цепи переменного тока
Если конденсатор включить в цепь постоянного тока, то такая цепь будет разомкнутой, так как обкладки конденсатора разделяет диэлектрик, и ток в цепи идти не будет. Иначе происходит в цепи переменного тока. Переменный ток способен течь в цепи, если она содержит конденсатор. Это происходит не из-за того, что заряды вдруг получили возможность перемещаться между пластинами конденсатора. В цепи переменного тока происходит периодическая зарядка и разрядка конденсатора, который в нее включен благодаря действию переменного напряжения.
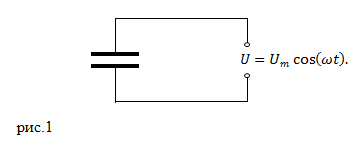
Рассмотрим цепь на рис.1, которая включает конденсатор. Будем считать, что сопротивление проводов и обкладок конденсатора не существенно, напряжение переменного тока изменяется по гармоническому закону:
![]()
По определению емкость на конденсаторе равна:
![]()
Следовательно, напряжение на конденсаторе:
![]()
Из выражения (3), очевидно, что заряд на конденсаторе будет изменяться по гармоническому закону:
![]()
Сила тока равна:
![]()
Сравнивая законы колебаний напряжения на конденсаторе и силы тока, видим, что колебания тока опережают напряжение на ![]() . Этот факт отражает то, что в момент начала зарядки конденсатора сила тока в цепи является максимальной при равенстве нулю напряжения. В момент времени, когда напряжение достигает максимума, сила тока падает до нуля.
. Этот факт отражает то, что в момент начала зарядки конденсатора сила тока в цепи является максимальной при равенстве нулю напряжения. В момент времени, когда напряжение достигает максимума, сила тока падает до нуля.
В течение ![]() периода, при зарядке конденсатора до максимального напряжения, энергия, поступающая в цепь, запасается на конденсаторе, в виде энергии электрического поля. За следующую четверть периода данная энергия возвращается обратно в цепь, когда конденсатор разряжается.
периода, при зарядке конденсатора до максимального напряжения, энергия, поступающая в цепь, запасается на конденсаторе, в виде энергии электрического поля. За следующую четверть периода данная энергия возвращается обратно в цепь, когда конденсатор разряжается.
Амплитуда силы тока (![]() ), исходя из выражения (5), равна:
), исходя из выражения (5), равна:
![]()
Емкостное сопротивление конденсатора
Физическую величину, равную обратному произведению циклической частоты на емкость конденсатора называют его емкостным сопротивлением (![]() ):
):
![]()
Роль емкостного сопротивления уподобляют роли активного сопротивления (R) в законе Ома:
![]()
где ![]() – амплитудное значение силы тока;
– амплитудное значение силы тока; ![]() – амплитуда напряжения. Для емкостного сопротивления действующая величина силы тока имеет связь с действующим значением напряжения аналогичную выражению (8) (как сила тока и напряжение для постоянного тока):
– амплитуда напряжения. Для емкостного сопротивления действующая величина силы тока имеет связь с действующим значением напряжения аналогичную выражению (8) (как сила тока и напряжение для постоянного тока):
![]()
На основании (9) говорят, что ![]() сопротивление конденсатора переменному току.
сопротивление конденсатора переменному току.
При увеличении емкости конденсатора растет ток перезарядки. Тогда как сопротивление конденсатора постоянному току является бесконечно большим (в идеальном случае), ёмкостное сопротивление конечно. С увеличением емкости и (или) частоты ![]() уменьшается.
уменьшается.
Примеры решения задач
| Задание | Если взять три конденсатора, имеющих емкость по C Ф каждый, соединить их параллельно, подключить в сеть с напряжением 220 В сколько электрической энергии будет потреблять такое соединение, если сопротивление проводов и обкладок конденсатора не учитывать?
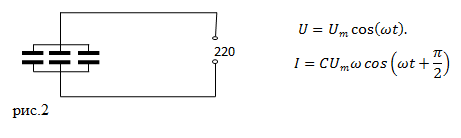
|
| Решение | Напряжение на пластинах конденсатора отстает от силы тока по фазе на при разности фаз |
| Ответ | В идеальном случае соединение конденсаторов электрической энергии потреблять не будет. |
| Задание | Конденсатор какой емкости следует включить в цепь переменного тока, если напряжение сети UВ, сила тока I А, частота колебаний в сети |
| Решение | Основой для решения задачи служит выражение:
где емкостное сопротивление (
|
| Ответ |











