Энтропия в термодинамике

Понятие энтропии в термодинамике

Понятие энтропии ввел в XIX веке Р. Клаузиус. Энтропия ( $S$ ) – это функция состояния, в обратимом процессе дифференциалом которой является величина $\frac{\delta Q}{T}$ :

$dS=\frac{\delta Q}{T} \qquad (1)$

где $\delta Q$ – количество теплоты, полученное термодинамической системой в ходе обратимого процесса; $T$ – термодинамическая температура системы.

В любом обратимом круговом процессе изменение энтропии равно нулю:

$\Delta S=0\ \qquad (2)$

Энтропия системы, которая совершает необратимый цикл, растет:

$\Delta S>0\ \qquad (3)$

Выражения (2) и (3) относятся только к замкнутым системам, в том случае, если система обменивается теплотой с внешней средой, то энтропия может вести себя как угодно. Формулы (2) и (3) в единстве представляют собой неравенство Клаузиуса:

$\Delta S\ge 0\ \qquad (4)$

которое говорит о том, что в замкнутых системах при обратимых процессах, энтропия остается постоянной, а в необратимых процессах она растет.

В случае равновесного перехода из одного состояния в другое, в соответствии с определением энтропии (1), имеем:

$\Delta S=S_2-S_1=\int^2_1{\frac{\delta Q}{T}=\int^2_1{\frac{dU+\delta A}{T}}} \qquad (5)$

где $\delta Q=dU+\delta A$ по первому началу термодинамики. $dU$ – изменение внутренней энергии термодинамической системы; $\delta A$ – работа выполняемая системой. В формуле (5) подынтегральное выражение и пределы интегрирования следует выразить, используя параметры, которые характеризуют процесс, происходящий в термодинамической системе. Выражение (5) определяет энтропию с точностью до аддитивной постоянной. Физический смысл несет изменение энтропии, а не сама энтропия.

Свойство энтропии

Энтропия имеет свойство аддитивности: Энтропия совокупности тел равна сумме энтропий каждого тела, которое входит в систему.

Глубинный смысл энтропии открывает статистическая физика. Больцман установил, что энтропия системы связана с термодинамической вероятностью ( $W$ ):

$S=k\ ln\ W\ \qquad (6)$

где $k$ – постоянная Больцмана.

Напомним, что термодинамической вероятностью называют число способов, при помощи которых можно реализовать макросостояние термодинамической системы, или количество микросостояний, которые реализуют данное макросостояние.

В соответствии с (6) энтропия — это мера вероятности состояния термодинамической системы. Иногда, исходя из статистического толкования энтропии, говорят, что энтропия – мера неупорядоченности системы.

Примеры решения задач

ПРИМЕР 1

Задание

Найдите изменение энтропии в процессах идеального газа.

Решение

В качестве основы для решения задачи используем формулу:

$\Delta S=\int^2_1{\frac{dU+\delta A}{T}\qquad (1.1)}$

Для идеального газа изменение внутренней энергии:

$dU=\frac{i}{2}\nu RdT\ \qquad (1.2)$

Работа газа по определению равна:

$\delta A=pdV\ \qquad (1.3)$

Или, если учесть, что из уравнения Менделеева – Клайперона:

$p=\frac{\nu RT}{V} \qquad (1.4)$

получаем, что элементарная работа идеального газа равна:

$\delta A=\frac{\nu RT}{V}dV \qquad (1.5)$

Подставим выражения (1.2) и (1.5) в определение изменения энтропии (1.1), получим:

$\Delta S=\int^{T_2}_{T_1}{\frac{i}{2}\frac{\nu RdT}{T}+\int^{V_2}_{V_1}{\frac{\nu RdV}{V}}=\nu R(\frac{i}{2}{\ln \left(\frac{T_2}{T_1}\right)+{\ln \left(\frac{V_2}{V_1}\right))}}} \qquad (1.6)$

Изменение энтропии при переходе из одного состояния в другое для идеального газа не зависит от процесса перехода.

Ответ

$\Delta S=\nu R(\frac{i}{2}{\ln \left(\frac{T_2}{T_1}\right)+{\ln \left(\frac{V_2}{V_1}\right))}}$

ПРИМЕР 2

Задание

Идеальный газ (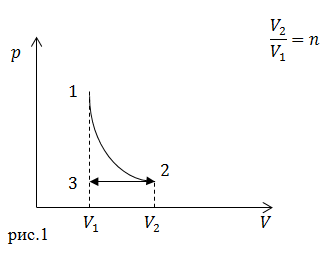 $i$ – число степеней свободы молекулы газа) расширили по адиабате (процесс 1-2), причем $\frac{V_2}{V_1}=n$ , после этого изобарно сжали до первоначального объема (рис.1). Каково изменение энтропии газа в результате проведенных процессов?

Решение

Так как энтропия является функцией состояния, то ее изменение в процессах перехода от точки 1-2-3 можно заменить на изменение энтропии в переходе 1-3. То есть:

$\Delta S_{1-2-3}=\Delta S_{1-3}=S_3-S_1 \qquad (2.1)$

В качестве основы для решения задачи воспользуемся формулой, которую мы получили в примере 1:

$\Delta S=\nu R(\frac{i}{2}{\ln \left(\frac{T_3}{T_1}\right)+{\ln \left(\frac{V_3}{V_1}\right))}} \qquad (2.2)$

Для изохорного процесса выражение (2.2) принимает вид:

$\Delta S=\nu R\frac{i}{2}{\ln \left(\frac{T_3}{T_1}\right)} \qquad (2.3)$

Так как процесс 3-1 изохорный, то для него справедлив закон Шарля:

$\frac{T_3}{T_1}=\frac{p_3}{p_1} \qquad (2.4)$

Воспользуемся уравнением адиабаты для процесса 1-2, и учтем, что процесс 2-3 изобарный, запишем:

$p_1V^{\gamma }_1=p_2V^{\gamma }_2=p_3V^{\gamma }_2\to \frac{p_3}{p_1}={\left(\frac{V_1}{V_2}\right)}^{\gamma }=n^{-\gamma } \qquad (2.5)$

Подставим правую часть выражения (2.5) вместо отношения $\frac{p_3}{p_1}$ в формулу (2.3), примем во внимание, что $\gamma =\frac{i+2}{i}$ имеем:

$\Delta S=\nu R\frac{i}{2}{\ln \left(\frac{T_3}{T_1}\right)=\nu R\frac{i}{2}\left(-\gamma \right){\ln n=-\nu R\frac{i+2}{2}}{\ln (n)}}$

Ответ

$\Delta S=-\nu R\frac{i+2}{2}{\ln (n)}$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Энтропия в термодинамике

Понятие энтропии в термодинамике

Свойство энтропии

Примеры решения задач