Как найти векторное произведение векторов?

DWQA Questions › Как найти векторное произведение векторов?

0 +1 -1

Asya Админ. спросил 7 лет назад

Здравствуйте! Нужна помощь по высшей математике. Вопрос звучит так: «Как найти векторное произведение векторов». Нужно коротко и четко объяснить, что такое векторное произведение векторов и проиллюстрировать с помощью примеров.

1 ответ

0 +1 -1

Asix Админ. ответил 7 лет назад

Пусть два вектора заданы координатами $\vec{a}=\left(a_{1}; a_{2}; a_{3}\right)$ и $\vec{b}=\left(b_{1}; b_{2}; b_{3}\right)$ .
Векторное произведение данных векторов обозначается $\left[\vec{a}, \vec{b}\right]$ или $\vec{a}\times\vec{b}$ и равно следующему определителю:

$\left[\vec{a}, \vec{b}\right]=\begin{vmatrix} \vec{i}&\vec{j}&\vec{k} \\ a_{1}&a_{2}&a_{3} \\ b_{1}&b_{2}&b_{3} \end{vmatrix}$

В результате расчета векторного произведения получается вектор.
Данный определитель чаще всего раскладывают по элементам первой строки.

Пример
Даны векторы $\vec{x}=\left(-\frac{1}{7}; 23; \sqrt{17}\right)$ , $\vec{y}=\left(\frac{1}{7}; 0; -13\right)$ . Найдем их векторное произведение.

Решение. Используем формулу для нахождения векторного произведения:

$\left[\vec{a}, \vec{b}\right]=\begin{vmatrix} \vec{i}&\vec{j}&\vec{k} \\ a_{1}&a_{2}&a_{3} \\ b_{1}&b_{2}&b_{3} \end{vmatrix}$

Подставим соответствующие координаты данных векторов и получим:

$\left[\vec{a}, \vec{b}\right]=\begin{vmatrix} \vec{i}&\vec{j}&\vec{k} \\ -\frac{1}{7}&23&\sqrt{17} \\ \frac{1}{7}&0&-13 \end{vmatrix}$

Выполним разложение определителя по элементам первой строки:

$\left[\vec{a}, \vec{b}\right]=\begin{vmatrix} \vec{i}&\vec{j}&\vec{k} \\ -\frac{1}{7}&23&\sqrt{17} \\ \frac{1}{7}&0&-13 \end{vmatrix}=\begin{vmatrix} 23&\sqrt{17} \\ 0&-13 \end{vmatrix}\cdot\vec{i}-\begin{vmatrix} -\frac{1}{7}&\sqrt{17} \\ \frac{1}{7}&-13 \end{vmatrix}\cdot\vec{j}+\begin{vmatrix} -\frac{1}{7}&23 \\ \frac{1}{7}&0 \end{vmatrix}\cdot\vec{k}=$

$=\left(23\cdot(-13)-\sqrt{17}\cdot0\right)\vec{i}-\left(-\frac{1}{7}\cdot(-13)-\sqrt{17}\cdot\frac{1}{7}\right)\vec{j}+\left(-\frac{1}{7}\cdot0-23\cdot\frac{1}{7}\right)\vec{k}=$

$=-299\vec{i}-\frac{13-\sqrt{17}}{7}\vec{j}-\frac{23}{7}\vec{k}$

Координаты вектора, который получают в результате векторного произведения, будут равны коэффициентам при единичных векторах $\vec{i}$ , $\vec{j}$ и $\vec{k}$ соответственно:

$\left[\vec{a}, \vec{b}\right]=\left(-299; -\frac{13-\sqrt{17}}{7}; -\frac{23}{7}\right).$

Ответ: $\left[\vec{a}, \vec{b}\right]=\left(-299; -\frac{13-\sqrt{17}}{7}; -\frac{23}{7}\right)$ .

Рассмотрим векторное произведение со стороны его геометрической интерпретации:
Площадь параллелограмма, который можно построить на векторах $\vec{a}$ и $\vec{b}$ , равна модулю векторного произведения данных векторов:

$S_{paral}=|\vec{a}\times\vec{b}|$

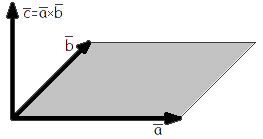
или половине треугольника, который построен та данных векторах:

$S_{\Delta}=\frac{1}{2}|\vec{a}\times\vec{b}|.$

Как найти векторное произведение векторов?

Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.