Как найти объем конуса

DWQA Questions › Как найти объем конуса

0 +1 -1

Asya Админ. спросил 6 лет назад

Здравствуйте!
Как найти объем конуса? Нужны формулы и желательно пример расчета.
Спасибо!

1 ответ

0 +1 -1

Asix Админ. ответил 6 лет назад

Рассмотрим конус с радиусом основания radius и высотой visota.

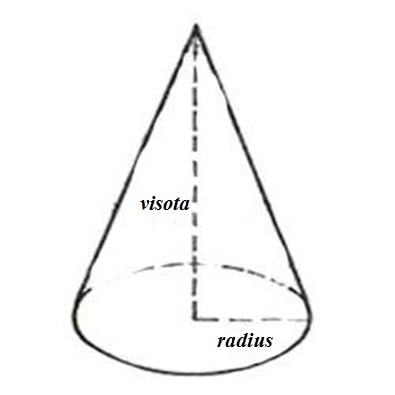
Объем конуса вычисляется через его высоту и радиус основания. Формула объема конуса выглядит так:

$V_{konusa}=\frac{1}{3}\pi \cdot visota\cdot {radius}^2$

Можно также записать формулу объема конуса через его диаметр:

$V_{konusa}=\frac{1}{12}\pi \cdot visota\cdot {diametr}^2$

Это основные формулы, которые используются для вычисления объема конуса.
Рассмотрим задачу на вычисление объема конуса.

Задача.
Радиус основания конуса равен 3 см, а его образующая равна 5 см. Найти объем конуса.

Решение.
Запишем формулу для вычисления объема конуса через радиус основания:

$V_{konusa}=\frac{1}{3}\pi \cdot visota\cdot {radius}^2$

Для использования этой формулы из условия известен размер радиуса, а высота неизвестна.
Рассмотрим прямоугольный треугольник, который образуется высотой, радиусом и образующей конуса. Используем теорему Пифагора и получим из данного треугольника следующее:

${obrazuyuschaya}^2={visota}^2+{radius}^2$

Выразим из формулы высоту:

${visota}^2={obrazuyuschaya}^2-{radius}^2$

$visota=\sqrt{{obrazuyuschaya}^2-{radius}^2}$

Подставим известные величины в формулу и получим:
$visota=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4$ (см).
Вычисленное значение высоты подставим в формулу объема:
$V_{konusa}=\frac{1}{3}\pi \cdot visota\cdot {radius}^2=\frac{1}{3}\pi \cdot 4\cdot 3^2=12\pi$ (куб. см).

Ответ. $12\pi$ куб. см.

Как найти объем конуса

Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.