Решение примеров со степенями
Для преобразования выражений со степенями используют свойства степеней, показательные тождества и формулы сокращенного умножения.
Основные свойства степеней: Для любых ![]() и положительных
и положительных ![]() и
и ![]() верны равенства
верны равенства
Примеры
| Задание | Найти значение выражения
|
| Решение | Основание каждого множителя можно представить в виде степени с основанием 5. Получим:
По свойствам степеней |
| Ответ |
| Задание | Вычислить
|
| Решение | Преобразуем, степени в числителе по свойству Далее воспользуемся тем фактом, что при умножении степеней с одинаковыми основаниями показатели степеней складываются Используя свойства степеней: |
| Ответ | 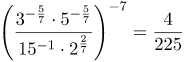 |
| Задание | Упростить пример со степенями
|
| Решение | Первые два множителя преобразуем в разность квадратов:
В последнем равенстве первые два множителя так же можно преобразуем в разность квадратов, получим: Последнее произведение является разностью кубов, преобразовав его, окончательно получим: |
| Ответ | 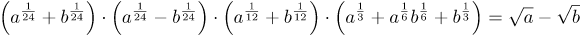 |
| Задание | Сократить пример со степенями
|
| Решение | Вынесем в числителе дроби за скобки и сократим числитель и знаменатель на два одинаковых выражения |
| Ответ | 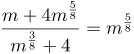 |
| Задание | Упростить выражения
|
| Решение | Приведем дроби к общему знаменателю.
|
| Ответ | 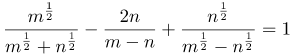 |






![Rendered by QuickLaTeX.com \[ \left( \frac{3^{-\frac{5}{7}} \cdot 5^{-\frac{5}{7}}}{15^{-1} \cdot 2^{\frac{2}{7}}} \right)^{-7} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9adcac1b84adc1d4cff55192e8b781ab_l3.png)
![Rendered by QuickLaTeX.com \[ \left( \frac{3^{-\frac{5}{7}} \cdot 5^{-\frac{5}{7}}}{15^{-1} \cdot 2^{\frac{2}{7}}} \right)^{-7} = \left( (3 \cdot 5)^{-\frac{5}{7}} \cdot 15^{1} \cdot 2^{-\frac{2}{7}} \right)^{-7} = \left( 15^{-\frac{5}{7}} \cdot 15^{1} \cdot 2^{-\frac{2}{7}} \right)^{-7} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-06478d005de8cd3c61dfc3875305fbf1_l3.png)
![Rendered by QuickLaTeX.com \[ \left( \frac{3^{-\frac{5}{7}} \cdot 5^{-\frac{5}{7}}}{15^{-1} \cdot 2^{\frac{2}{7}}} \right)^{-7} = \left( 15^{-\frac{5}{7}} \cdot 15^{1} \cdot 2^{-\frac{2}{7}} \right)^{-7} = \left( 15^{1-\frac{5}{7}} \cdot 2^{-\frac{2}{7}} \right)^{-7} = \left( 15^{\frac{2}{7}} \cdot 2^{-\frac{2}{7}} \right)^{-7} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2cb62f28e1575c9255ad67da590c4eae_l3.png)
![Rendered by QuickLaTeX.com \[ \left( \frac{3^{-\frac{5}{7}} \cdot 5^{-\frac{5}{7}}}{15^{-1} \cdot 2^{\frac{2}{7}}} \right)^{-7} = \left( 15^{\frac{2}{7}} \cdot 2^{-\frac{2}{7}} \right)^{-7} = \left( 15^{\frac{2}{7}} \right)^{-7} \cdot \left( 2^{-\frac{2}{7}} \right)^{-7} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7dd371231076eddc1ac7d41dd67c23e7_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{m+4m^{\frac{5}{8}}}{m^{\frac{3}{8}}+4} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5aa2d2dd6ae7e3f488af446e7f08845f_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{m+4m^{\frac{5}{8}}}{m^{\frac{3}{8}}+4} = \frac{m^{\frac{5}{8}} \left( m^{\frac{3}{8}}+4 \right)}{m^{\frac{3}{8}}+4} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-68f51d129c3e3a8eefcf4f9b73f344a5_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{m+4m^{\frac{5}{8}}}{m^{\frac{3}{8}}+4} = \frac{m^{\frac{5}{8}} \left( m^{\frac{3}{8}}+4 \right)}{m^{\frac{3}{8}}+4} = m^{\frac{5}{8}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ed401e91286d22307407b64017958d62_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{m^{\frac{1}{2}}}{m^{\frac{1}{2}} + n^{\frac{1}{2}}} - \frac{2n}{m-n} + \frac{n^{\frac{1}{2}}}{m^{\frac{1}{2}} - n^{\frac{1}{2}}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9a012ea7516f85c8eeb09cbf0671ba62_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{m^{\frac{1}{2}}}{m^{\frac{1}{2}} + n^{\frac{1}{2}}} - \frac{2n}{m-n} + \frac{n^{\frac{1}{2}}}{m^{\frac{1}{2}} - n^{\frac{1}{2}}} = \frac{m^{\frac{1}{2}} \left( m^{\frac{1}{2}} - n^{\frac{1}{2}} \right) - 2n + n^{\frac{1}{2}} \left( m^{\frac{1}{2}} + n^{\frac{1}{2}} \right)}{m-n} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-91bfdc52790f4fa5f1a80a1cecc7d72f_l3.png)





