Решение примеров с корнями
При преобразовании выражений с корнями используют определение и свойство арифметического корня ![]() -ой степени, свойства степени с рациональным показателем, а так же правила внесения множителя под знак корня и вынесения множителя из под знака корня. При этом разделяют случаи четной и нечетной степени корня.
-ой степени, свойства степени с рациональным показателем, а так же правила внесения множителя под знак корня и вынесения множителя из под знака корня. При этом разделяют случаи четной и нечетной степени корня.
| Задание | Найти значение выражения
|
| Решение | По свойству арифметического квадратного корня |
| Ответ |
| Задание | Вычислить пример с корнем
|
| Решение | По свойству арифметического квадратного корня Найдем значение модулей, используя определение, получим: |
| Ответ |
| Задание | Упростить выражение с корнем
|
| Решение | Запишем показатели степеней рациональными числами и преобразуем их:
|
| Ответ | 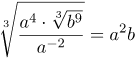 |
| Задание | Вычислить
|
| Решение | Избавимся от иррациональности в первой дроби, для этого умножим числитель и знаменатель дроби на выражение сопряженное со знаменателем, то есть на Полученную дробь преобразуем, используя формулы сокращенного умножения: Далее вычтем дроби, для этого приведем их сначала к общему знаменателю: |
| Ответ | 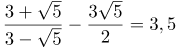 |
| Задание | Вычислить
|
| Решение | Представим подкоренное выражение в виде:
Таким образом, подкоренное выражение представляет собой квадрат суммы: По свойству арифметического квадратного корня Полученное выражение представляет собой разность квадратов, свернем его: |
| Ответ | 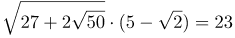 |






![Rendered by QuickLaTeX.com \[ \sqrt[3]{\frac{a^{4} \cdot \sqrt[3]{b^{9}}}{a^{-2}}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9351625222e6182124c8e5a318388104_l3.png)
![Rendered by QuickLaTeX.com \[ \sqrt[3]{\frac{a^{4} \cdot \sqrt[3]{b^{9}}}{a^{-2}}} = \left( a^{4-(-2)} \cdot b^{\frac{9}{3}} \right)^{\frac{1}{3}} = \left( a^{6} \cdot b^{3} \right)^{\frac{1}{3}} = \left( a^{6} \right)^{\frac{1}{3}} \cdot \left( b^{3} \right)^{\frac{1}{3}} = a^{\frac{6}{3}} \cdot b^{\frac{3}{3}} = a^{2}b \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-cd4de38ab0b05b325a7c66f3276a8569_l3.png)





