Примеры решения второй замечательный предел
Предел
![]()
называется вторым замечательным пределом. Он разрешает неопределенность вида ![]() и имеет следующие основные следствия
и имеет следующие основные следствия
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \left( 1 + \frac{k}{x} \right)^{x} =e^{k} \text{ }\text{ },\text{ }\text{ } \lim_{x \rightarrow \infty} \left( 1 + \frac{1}{f(x)} \right)^{f(x)} =e \text{ }\text{ },\text{ }\text{ } \lim_{x \rightarrow \infty} \left( 1 + x \right)^{\frac{1}{x}} =e \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7f8a4cd5327eec4ec42e324ed1777de7_l3.png)
| Задание | Вычислить предел
|
| Решение | Поделим почленно числитель на знаменатель:
Получаем неопределенность получим: |
| Ответ | 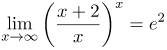 |
| Задание | Вычислить предел
|
| Решение | Представим числитель в виде суммы:
затем поделим почленно числитель на знаменатель, получим: Получили неопределенность По следствию из второго замечательного предела выражение выделим его, в рассматриваем пределе: |
| Ответ | 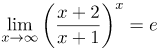 |
| Задание | Вычислить предел
|
| Решение | Имеем неопределенность По следствию из второго замечательного предела подставляя это значение в предел, будем иметь: |
| Ответ | 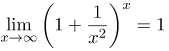 |
Приведем несколько примеров пределов, которые по формулировке похожи на второй замечательный предел, но таковыми не являются.
| Задание | Вычислить предел
|
| Решение | Найдем предел выражения в скобках
Тогда заданный предел будет равен так как |
| Ответ | 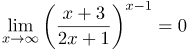 |
| Задание | Вычислить предел
|
| Решение | Вычислим предел выражения в скобках
Тогда предел всего выражения равен: так как |
| Ответ | 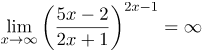 |






![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \left( \frac{x+2}{x+1} \right)^{x} = \lim_{x \rightarrow \infty} \left(1+ \frac{1}{x+1} \right)^{x} = \lim_{x \rightarrow \infty} \left(1+ \frac{1}{x+1} \right)^{\frac{x(x+1)}{x+1}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6cc74e6b3c049a5b2f2ea8698b4f91af_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \left( \frac{x+2}{x+1} \right)^{x} = \lim_{x \rightarrow \infty} \left(1+ \frac{1}{x+1} \right)^{x} = \lim_{x \rightarrow \infty} \left[ \left(1+ \frac{1}{x+1} \right)^{x+1} \right] ^{\frac{x}{x+1}} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ef0435407127943e758ff56a630168a8_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \left(1+ \frac{1}{x^{2}} \right)^{x} = \lim_{x \rightarrow \infty} \left(1+ \frac{1}{x^{2}} \right)^{\frac{x \cdot x}{x}} = \lim_{x \rightarrow \infty} \left[ \left(1+ \frac{1}{x^{2}} \right)^{x^{2}} \right] ^{\frac{1}{x}} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-922783be4d13cb0e2381334d2fd972ef_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \left( 1+\frac{1}{x^{2}} \right)^{x^{2}} = e \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2207f483d10ee8cb8d70fdfd48fd30d6_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \left(1+ \frac{1}{x^{2}} \right)^{x} = \lim_{x \rightarrow \infty} \left[ \left(1+ \frac{1}{x^{2}} \right)^{x^{2}} \right] ^{\frac{1}{x}} = \lim_{x \rightarrow \infty} e^{\frac{1}{x}} = e^{0}=1 \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-101594a3ca07561652090d528714494c_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \frac{x+3}{2x+1} = \lim_{x \rightarrow \infty} \frac{x \left( 1+\frac{3}{x} \right) }{x \left( 2+\frac{1}{x} \right)} = \lim_{x \rightarrow \infty} \frac{1+\frac{3}{x}}{2+\frac{1}{x}} = \frac{1+0}{2+0} = \frac{1}{2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eb55c79ff79d7f47a0acbcdc4167fd06_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \frac{5x-2}{2x+1} = \lim_{x \rightarrow \infty} \frac{x \left( 5 - \frac{2}{x} \right)}{x \left( 2+\frac{1}{x} \right)} = \lim_{x \rightarrow \infty} \frac{5 - \frac{2}{x}}{2+\frac{1}{x}} = \frac{5-0}{2+0}=\frac{5}{2} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f61d2f889d4f9b575146f8fd5bf12a75_l3.png)





