Примеры решения пределов с корнями
Пределы с корнями могут подпадать под случай отношения двух многочленов, когда ![]() и тогда сравниваются старшие степени числителя и знаменателя. Если же при вычислении предела с корнями получается неопределенность
и тогда сравниваются старшие степени числителя и знаменателя. Если же при вычислении предела с корнями получается неопределенность ![]() , то в этом случае, чаще всего, избавляются от иррациональности, умножая числитель и знаменатель дроби на сопряженное к выражению, содержащему иррациональность.
, то в этом случае, чаще всего, избавляются от иррациональности, умножая числитель и знаменатель дроби на сопряженное к выражению, содержащему иррациональность.
| Задание | Вычислить предел
|
| Решение | Подставим значение |
| Ответ | 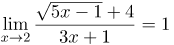 |
| Задание | Вычислить предел с корнем
|
| Решение | Так как |
| Ответ | 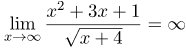 |
| Задание | Вычислить предел
|
| Решение | Старшая степень числителя совпадает со старшей степенью знаменателя и равна |
| Ответ | 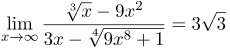 |
| Задание | Вычислить предел с корнем
|
| Решение | Подставим значение Получили неопределенность Свернем числитель, используя формулы сокращенного умножения, получим разность квадратов: Сократим полученную дробь на Далее подставляя значение |
| Ответ | 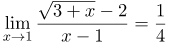 |
| Задание | Вычислить предел
|
| Решение | Если подставить значение то получим неопределенность Выражение, получившееся в числителе, есть разность квадратов, свернем его: Упростим полученное выражение: В последнее выражение подставим значение |
| Ответ | 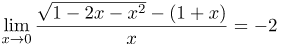 |






![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \frac{x^{2}+3x+1}{\sqrt{x+4}} = \lim_{x \rightarrow \infty} \frac{x^{2} \cdot \left( \frac{x^{2}}{x^{2}} + \frac{3x}{x^{2}} - \frac{1}{x^{2}}\right)}{x^{2} \sqrt{\frac{x}{x^{4}} + \frac{4}{x^{4}}}} = \lim_{x \rightarrow \infty} \frac{1 + \frac{3}{x} -\frac{1}{x^{2}}}{\sqrt{\frac{1}{x^{3}} + \frac{4}{x^{4}}}} = \left[ \frac{1}{0} \right] = \infty \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-7447b733bd295a6d6ab200a9ae80b486_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow \infty} \frac{\sqrt[3]{x}-9x^{2}}{3x - \sqrt[4]{9x^{8}+1}} = \lim_{x \rightarrow \infty} \frac{x^{2} \cdot \left( \frac{\sqrt[3]{x}}{x^{2}} -9 \right) }{x^{2} \cdot \left( \frac{3}{x} -\sqrt[4]{9+\frac{1}{x^{8}}} \right) } = \lim_{x \rightarrow \infty} \frac{\frac{1}{x \cdot \sqrt[3]{x^{2}}}-9}{\frac{3}{x} -\sqrt[4]{9+\frac{1}{x^{8}}}} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2371dcf820a5750c812a1d093e7a9585_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow 1} \frac{\sqrt{3+x}-2}{x-1} = \lim_{x \rightarrow 1} \frac{(\sqrt{3+x}-2)(\sqrt{3+x}+2)}{(x-1)(\sqrt{3+x}+2)} = \lim_{x \rightarrow 1} \frac{\left( \sqrt{3+x} \right)^{2}-2^{2}}{(x-1)(\sqrt{3+x}+2)} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4f64455866e576f56940e2ed9eec8ae9_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow 0} \frac{\sqrt{1-2x-x^{2}}-(1+x)}{x} = \lim_{x \rightarrow 0} \frac{ \left( \sqrt{1-2x-x^{2}}-(1+x)\right) \left( \sqrt{1-2x-x^{2}}+(1+x)\right)}{x\left( \sqrt{1-2x-x^{2}}+(1+x)\right)} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-221b8efd65b02248e8f9c2ee83296aa1_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow 0} \frac{\sqrt{1-2x-x^{2}}-(1+x)}{x} = \lim_{x \rightarrow 0} \frac{ \left( \sqrt{1-2x-x^{2}}-(1+x)\right) \left( \sqrt{1-2x-x^{2}}+(1+x)\right)}{x\left( \sqrt{1-2x-x^{2}}+(1+x)\right)} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-16f8bf14bf9f9254e7717d8e538a5766_l3.png)
![Rendered by QuickLaTeX.com \[ = \lim_{x \rightarrow 0} \frac{ \left( \sqrt{1-2x-x^{2}} \right)^{2} - (1+x^{2})}{x\left( \sqrt{1-2x-x^{2}}+(1+x)\right)} \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e063817976ebd5c6f7070854716990a3_l3.png)
![Rendered by QuickLaTeX.com \[ \lim_{x \rightarrow 0} \frac{\sqrt{1-2x-x^{2}}-(1+x)}{x} = \lim_{x \rightarrow 0} \frac{ \left( \sqrt{1-2x-x^{2}} \right)^{2} - (1+x^{2})}{x\left( \sqrt{1-2x-x^{2}}+(1+x)\right)} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9d7968f077eb3676187c55671551b1e4_l3.png)
![Rendered by QuickLaTeX.com \[ = \lim_{x \rightarrow 0} \frac{1-2x-x^{2}-1-2x-x^{2}}{x\left( \sqrt{1-2x-x^{2}}+(1+x)\right)} = \lim_{x \rightarrow 0} \frac{-4x-2x^{2}}{x\left( \sqrt{1-2x-x^{2}}+(1+x)\right)} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8bf5c20e18d84146dc5d8fab45e01b73_l3.png)
![Rendered by QuickLaTeX.com \[ = \lim_{x \rightarrow 0} \frac{x(-4-2x)}{x\left( \sqrt{1-2x-x^{2}}+(1+x)\right)} = \lim_{x \rightarrow 0} \frac{-4-2x}{\sqrt{1-2x-x^{2}}+(1+x)} = \]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-749b359ad69aec90ef58563b4895b112_l3.png)





