Примеры решения логарифмов
Теория про логарифмы
То есть, если ![]() , где
, где ![]() и
и ![]() , то
, то ![]() .
.
Логарифм по основанию 10 называется десятичным логарифмом и обозначается ![]() :
:
![]()
а логарифм по основанию ![]() называют натуральным и обозначают
называют натуральным и обозначают ![]() :
:
![]()
Примеры
| Задание | Найти значение выражения |
| Решение | Представим основание и число, находящиеся под логарифмом, в виде степени 2, получим:
Выносим степени из под знака логарифма, как коэффициент, согласно формулам Учитывая, что |
| Ответ | 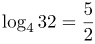 |
| Задание | Найти значение выражения |
| Решение | Сумма логарифмов равна логарифму произведения, поэтому данное выражение перепишется в виде:
Учитывая, что |
| Ответ |
| Задание | Вычислить значение выражения
|
| Решение | Перейдем в каждом из слагаемых к логарифму по основанию 18, используя формулу перехода Так как сумма логарифмов равна логарифму произведения, последняя сумма перепишется в виде: Число 324 можно представить как степень 18, получим далее выносим степень как коэффициент перед знаком логарифма: Учитывая, что |
| Ответ | 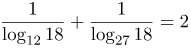 |
| Задание | Вычислить |
| Решение | Представим 8 и 9 как степень соответственно 2 и 3:
Внесем коэффициенты перед логарифмами как степень подлогарифмического выражения: Использую основное логарифмическое тождество |
| Ответ |
| Задание | Вычислить |
| Решение | Перейдем во всех логарифмах к основанию 2, используя формулу перехода к новому основанию:
получим Представим 4 и 8 в виде степени двойки и вынесем полученные степени за знак логарифма как коэффициент: |
| Ответ | 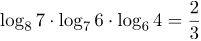 |











