Примеры решения квадратных уравнений

Теория по квадратным уравнениям

ОПРЕДЕЛЕНИЕ

Квадратным уравнением называется уравнение вида $ax^{2}+bx+c=0$ , где $a \neq 0$ .

Возможны такие случаи:

$1) \text{ } c=0 \text{ };\text{ } b \neq 0$ , тогда имеем квадратное уравнение вида $ax^{2}+bx=0 \text{ } \Rightarrow \text{ } x(ax+b)=0 \text{ } \Rightarrow \text{ } x_{1}=0$ и $x_{2}=-\frac{b}{a}$ .

$2) \text{ } c \neq 0 \text{ };\text{ } b = 0$ , тогда имеем квадратное уравнение вида $ax^{2}+c=0 \text{ } \Rightarrow \text{ } ax^{2}=-c \text{ } \Rightarrow \text{ } x = -\frac{c}{a} \text{ } ; \text{ } x_{1,2} = \sqrt{-\frac{c}{a}}$ , если $\frac{c}{a} < 0$ ; если $\frac{c}{a} > 0$ – корней нет.

$3) \text{ } c = 0 \text{ };\text{ } b = 0$ , тогда имеем квадратное уравнение вида $ax^{2}=0 \text{ } \Rightarrow \text{ } x_{1,2}=0$ .

$4) \text{ } c \neq 0 \text{ };\text{ } b \neq 0$ , тогда имеем полное квадратное уравнение $ax^{2}+bx+c=0$ , которое решается или с помощью дискриминанта:

$D = b^{2}-4ac \text{ } \Rightarrow \text{ } x_{1,2} = \frac{-b \pm \sqrt{D}}{2a}$

Или по теореме Виета:

$x_{1}+x_{2} = -b \text{ } ; \text{ } x_{1} \cdot x_{2} = c$

Примеры

ПРИМЕР 1

Задание

Решить следующие неполные квадратные уравнения

$1) \text{ } 2x^{2}-4x=0 \text{ } ; \text{ } 2) \text{ } 2x^{2}-18=0 \text{ } ; \text{ } 3) \text{ } 3x^{2}+27=0 \text{ } ; \text{ } 4) \text{ } 5x^{2}=0$

Решение

1) В уравнении $2x^{2}-4x=0$ вынесем $2x$ за скобки $2x(x-2)=0$ . Произведение равно нулю, если один из сомножителей равен нулю, следовательно:

$2x = 0 \text{ } \Rightarrow \text{ } x_{1}=0$

или

$x-2 = 0 \text{ } \Rightarrow \text{ } x_{2}=2$

2) В уравнении $2x^{2}-18=0$ перенесем свободный член вправо и раздели его на коэффициент при $x^{2}$ :

$2x^{2}=18 \text{ } \Rightarrow \text{ } x^{2}=9 \text{ } \Rightarrow \text{ } x = \pm \sqrt{9} \text{ } \Rightarrow \text{ } x_{1}=3 \text{ },\text{ } x_{2}=-3$

3) В уравнении $3x^{2}+27=0$ перенесем свободный член вправо и раздели его на коэффициент при $x^{2}$ :

$3x^{2}=27 \text{ } \Rightarrow \text{ } x^{2}=-9 \text{ }\text{ }\text{ }\text{ } - \oslash$

У данного квадратного уравнения нет корней.

4) уравнение $5x^{2}=0$ равносильно уравнению $x^{2}=0$ , которое имеет два совпадающих корня $x_{1}=x_{2}=0$ .

Ответ

$1) \text{ } x_{1}=0 \text{ },\text{ } x_{2}=2$

$2) \text{ } x_{1}=3 \text{ },\text{ } x_{2}=-3$

$3)\text{ }$ Корней нет

$4) \text{ } x_{1}=x_{2}=0$

ПРИМЕР 2

Задание

Решить квадратное уравнение $4x^{2}-4x+1=0$

Решение

Подсчитаем для заданного уравнения, чему равен дискриминант:

$D=(-4)^{2}-4 \cdot 4 \cdot 1 = 16-16=0$

Так как $D=0$ , то уравнение $4x^{2}-4x+1=0$ имеет два совпадающих корня:

$x_{1}=x_{2}=\frac{-(-4)}{2 \cdot 4} = \frac{1}{2}$

Ответ

ПРИМЕР 3

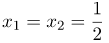Задание

Решить уравнение $x^{2}+2x+5=0$

Решение

Вычислим дискриминант для исходного уравнения, получим:

$D=2^{2}-4 \cdot 5 \cdot 1 = 4-20=-16$

Так как $D<0$ , данное уравнение решений не имеет.

Ответ

Корней нет.

ПРИМЕР 4

Задание

Решить квадратное уравнение $x^{2}+2x-48=0$

Решение

Дискриминант заданного уравнения, равен

$D=2^{2}-4 \cdot (-48) \cdot 1 = 4+192=196$

Следовательно, уравнение $x^{2}+2x-48=0$ имеет два различных корня

$x_{1,2}=\frac{-2 \pm \sqrt{196}}{2 \cdot 1} =\frac{-2 \pm 14}{2} \text{ } \Rightarrow \text{ } x_{1}=-8 \text{ },\text{ } x_{2}=6$

Ответ

$x_{1}=-8 \text{ },\text{ } x_{2}=6$

ПРИМЕР 5

Задание

Решить уравнение, используя теорему Виета: $x^{2}-x-12=0$

Решение

Пусть $x_{1}$ и $x_{2}$ – корни квадратного уравнения, по следствию из теоремы Виета

$x_{1}+x_{2}=1 \text{ }\text{ };\text{ }\text{ } x_{1} \cdot x_{2}=-12$

Проанализируем полученные равенства. Произведение корней отрицательно, следовательно, корни имеют разные знаки. Разложим –12 на множители, учитывая, что они должны быть числами разного знака. Возможны такие варианты: –12 и 1; 12 и –1; –6 и 2; 6 и –2; –4 и 3; 4 и –3. Так как сумма корней равна 1, то корнями будут числа $x_{1}=4$ и $x_{2}=-3$ .

Ответ

$x_{1}=4 \text{ },\text{ } x_{2}=-3$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Примеры решения квадратных уравнений

Теория по квадратным уравнениям

Примеры