Примеры решения дифференциальных уравнений

Теория по дифференциальным уравнениям

ОПРЕДЕЛЕНИЕ

Дифференциальное уравнение – это уравнение, в котором неизвестной является функция одной переменной, причем уравнение содержит не только неизвестную функцию, но и ее производные различных порядков. Порядок наивысшей производной, входящей в уравнение, называется порядком этого дифференциального уравнения.

Дифференциальные уравнения имеют большое прикладное значение: они широко используются в механике, астрономии, физике и других науках. Широкое распространение дифференциальных уравнений в естествознании объясняется тем, что многие явления и процессы, происходящие в природе, количественно описываются обыкновенными дифференциальными уравнениями.

При решении дифференциальных уравнений главной задачей является определить тип дифференциального уравнения, а затем четко следовать алгоритму решения дифференциальных уравнений этого типа.

Примеры

ПРИМЕР 1

Задание

Решить дифференциальное уравнение первого порядка $y dy - xy dx=0$

Решение

Данное дифференциальное уравнение является дифференциальным уравнением с разделяющимися переменными. Разделим переменные

$y dy = xy dx \text{ } \Rightarrow \text{ } \frac{ydy}{y} = x dx \text{ } \Rightarrow \text{ } dy = x dx$

Проинтегрируем левую и правую части последнего равенства

$\int dy = \int x dx \text{ } \Rightarrow \text{ } y = \frac{x^{2}}{2} + C$

Ответ

ПРИМЕР 2

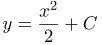Задание

Решить дифференциальное уравнение первого порядка $y'-y=2x-3$

Решение

Запишем уравнение в виде

$y'=y+2x-3$

Данное дифференциальное уравнение приводится к уравнению с разделяющимися переменными заменой $z=y+2x$ . Считая $z$ функцией от $x$ , получим:

$z'=y'+2 \cdot 1 - 0 \text{ } \Rightarrow \text{ } y'=z'-2$

Подставляя полученные выражения в первое уравнение, приходим к дифференциальному уравнению с разделяющимися переменными:

$z'-2=z-3 \text{ } \Rightarrow \text{ } z'=z-1 \text{ } \Rightarrow \text{ } \frac{dz}{dx}=z-1 \text{ } \Rightarrow \text{ } \frac{dz}{z-1} = dx$

Проинтегрируем обе части последнего равенства:

$\int \frac{dz}{z-1} = \int dx \text{ } \Rightarrow \text{ } \ln |z-1| = x+C$

Делая обратную замену, окончательно получим:

$\ln |y+2x-1| = x+C$

Ответ

$\ln |y+2x-1| = x+C$

ПРИМЕР 3

Задание

Решить дифференциальное уравнение $4x^{2}y'=4x^{2}+y^{2}$

Решение

Разделим обе части этого уравнения на $x^{2}$ , получим:

$4y'=4+\frac{y^{2}}{x^{2}}$

Данное дифференциальное уравнение является однородным. Введем замену

$u=\frac{y}{x} \text{ } \Rightarrow \text{ } y = u \cdot x \text{ } \Rightarrow \text{ } y'=u'x+u$

Подставляя замену в последнее уравнение, будем иметь:

$4(u'x+u)=4+u^{2}$

$4x \cdot u'+4u=4+u^{2}$

$4x \cdot u'=u^{2}-4u+4$

$4x \cdot \frac{du}{dx}=(u-2)^{2}$

$\frac{du}{(u-2)^{2}} = \frac{dx}{4x}$

Проинтегрируем обе части последнего равенства:

$\int \frac{du}{(u-2)^{2}} = \int \frac{dx}{4x} \text{ } \Rightarrow \text{ } \int \frac{d(u-2)}{(u-2)^{2}} = \frac{1}{4} \int \frac{dx}{x} \text{ } \Rightarrow \text{ } -\frac{1}{u-2} = \frac{1}{4} \ln |x| + \ln C$

$1 = (2-u) \ln \left( C \cdot \sqrt[4]{|x|} \right)$

Сделаем обратную замену $u=\frac{y}{x}$ :

$1 = \left( 2 - \frac{y}{x} \right) \ln \left( C \cdot \sqrt[4]{|x|} \right) \text{ } \Rightarrow \text{ } x = (2x-y) \ln \left( C \cdot \sqrt[4]{|x|} \right)$

Выразим из последнего уравнения $y$ :

$x = 2x \ln \left( C \cdot \sqrt[4]{|x|} \right) -y \ln \left( C \cdot \sqrt[4]{|x|} \right) \text{ } \Rightarrow \text{ } y \ln \left( C \cdot \sqrt[4]{|x|} \right) = 2x \ln \left( C \cdot \sqrt[4]{|x|} \right) - x$

$y = \frac{2x \ln \left( C \cdot \sqrt[4]{|x|} \right) - x}{\ln \left( C \cdot \sqrt[4]{|x|} \right)} \text{ } \Rightarrow \text{ } y = 2x - \frac{x}{\ln \left( C \cdot \sqrt[4]{|x|} \right)}$

Ответ

ПРИМЕР 4

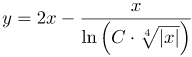Задание

Решить дифференциальное уравнение первого порядка

$y'-\frac{y}{x} = \frac{1}{x^{2}}$

Решение

Имеем линейное дифференциальное уравнение. Решение будем искать в виде произведения двух функций $y=u(x) \cdot v(x)$ , тогда по правилу дифференцирования произведения: $y'=u'v+uv'$ . Подставляя все в исходное уравнение, получим:

$u'v+uv'-\frac{uv}{x} = \frac{1}{x^{2}} \text{ } \Rightarrow \text{ } u'v+u \left( v' - \frac{v}{x} \right) = \frac{1}{x^{2}}$

Подберем функцию $v$ так, чтобы выражение в скобках было равно 0. Тогда имеет место система

$\begin{cases} v' - \frac{v}{x} =0\\ u'v = \frac{1}{x^{2}} \end{cases}$

Первое уравнение – дифференциальное уравнение с разделяющимися переменными:

$\frac{dv}{dx} = \frac{v}{x} \text{ } \Rightarrow \text{ } \int \frac{dv}{v} = \int \frac{dx}{x} \text{ } \Rightarrow \text{ } \ln |v| = \ln |x| + C$

Положим $C=0$ , тогда $v=x$ . Подставим найденное значение во второе уравнение и решим его:

$u'x = \frac{1}{x^{2}} \text{ } \Rightarrow \text{ } \frac{du}{dx} = \frac{1}{x^{3}} \text{ } \Rightarrow \text{ } \int du = \int x^{-3} dx \text{ } \Rightarrow \text{ } u = \frac{x^{-2}}{-2} + C \text{ } \Rightarrow \text{ } u = -\frac{1}{2x^{2}} + C$

Учитывая, что мы искали решение в виде $y=u(x) \cdot v(x)$ , искомая функция

$y = \left( -\frac{1}{2x^{2}} + C \right) \cdot x \text{ } \Rightarrow \text{ } y = -\frac{1}{2x} + Cx$

Ответ

ПРИМЕР 5

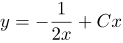Задание

Решить задачу Коши $y'+y \text{tg }x = \frac{1}{\cos x}$ при начальном условии $y(0)=1$ .

Решение

Данное дифференциальное уравнение является линейным. Его решение будем искать в виде $y=u(x) \cdot v(x)$ , тогда $y'=u'v+uv'$ . Подставим все в исходное уравнение, получим:

$u'v+uv'+uv \text{tg }x = \frac{1}{\cos x}$

$u'v+u \left(v'+ v \text{tg }x \right) = \frac{1}{\cos x}$

Функцию $v$ подбираем так, чтобы выражение в скобках равнялось 0. Имеет место система

$\begin{cases} v'+ v \text{tg }x =0\\ u'v = \frac{1}{\cos x} \end{cases}$

Первое дифференциальное уравнение является уравнением с разделяющимися переменными:

$v' =- v \text{tg }x \text{ } \Rightarrow \text{ } \frac{dv}{dx} = - v \text{tg }x \text{ } \Rightarrow \text{ } \int \frac{dv}{v} = - \int \text{tg } x dx \text{ } \Rightarrow \text{ } \ln |v| = - \int \frac{\sin x dx}{\cos x}$

$\ln |v| = \int \frac{d(\cos x)}{\cos x} \text{ } \Rightarrow \text{ } \ln |v| = \ln |\cos x| + C$

Полагая $C=0$ и потенцируя полученное уравнение по основанию $e$ , имеем, что $v= \cos x$ . Подставим найденное значение $v$ во второе уравнение системы:

$u' \cos x = \frac{1}{\cos x}$

Получили уравнение с разделяющимися переменными. Его решение

$\frac{du}{dx} = \frac{1}{\cos ^{2} x} \text{ } \Rightarrow \text{ } \int du = \int \frac{dx}{\cos ^{2} x} \text{ } \Rightarrow \text{ } u = \text{tg }x + C$

Учитывая, что решение ищется в виде $y=u(x) \cdot v(x)$ , получим:

$y = (\text{tg }x + C) \cos x \text{ } \Rightarrow \text{ } y = \sin x + C \cos x$

Используя начальное условие $y(0)=1$ , найдем значение константы интегрирования:

$1 = \sin 0 + C \cdot \cos 0 \text{ } \Rightarrow \text{ } 1=0+C \cdot 1 \text{ } \Rightarrow \text{ } C=1$

Таким образом, частное решение заданного уравнения будет иметь вид:

$y = \sin x + \cos x$

Ответ

$y = \sin x + \cos x$

Понравился сайт? Расскажи друзьям!

Советуем прочитать:

Примеры решения дифференциальных уравнений

Теория по дифференциальным уравнениям

Примеры